Fluide en équilibre statique
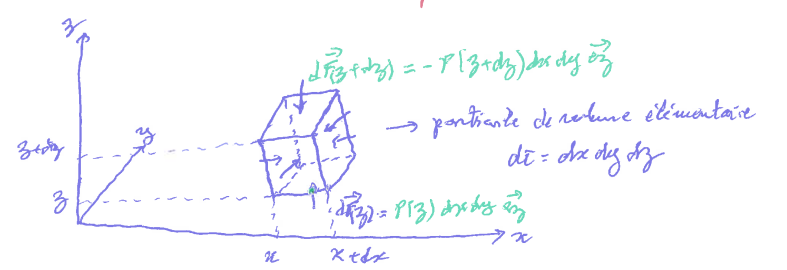
Forces:
Ces deux forces se compensent, c'est pourquoi le fluide est statique.
En mécanique des fluides, on préfère exprimer les forces volumiques.
Force volumique pressante
La force volumique préssante s'écrit:
$$\vec f_P={{\frac{d\vec F_P}{d\tau} }}=-\vec{grad}(P)$$
Avec:- \(\vec f_P\): la force volumique pressante en \(N.m^{-3}\)
Equation de la statique des fluides
Un fluide statique est un fluide immobile, c'est-à-dire un fluide dont toutes les forces se compensent.
En appliquant la
Deuxième loi de Newton - Principe fondamental de la dynamique pour une particule élémentaire:
$$\sum d\vec F_{ext}=dm.\vec a=\vec 0$$
$$dm.\vec g+d\vec F_P=\vec 0\qquad \text{(en absence d'autres forces)}$$
$$\rho d\tau\vec g-\vec{grad}(P)d\tau=\vec 0$$
Enoncé de l'équation de la statique des fluides
Cette équation découle de la Deuxième loi de Newton - Principe fondamental de la dynamique pour un fluide statique.
On trouve:
$$\vec{grad}P(M)={{\rho(M)\vec g}}$$
Cas d'un fluide incompressible
Un fluide est imcopressible \((\rho=cst)\) tant que la vitesse des ondes qui le traversent est petite devant la vitesse du son.
D'après l'
Equation de la statique des fluides:
$$dP=-\rho g dz$$
$$d(P+\rho g dz)=0$$
$$\implies P+\rho g z=cst\quad \text{en }J.m^{-3}$$
On en déduit que les "isobares" sont des surfaces horizontales.
Cela explique que les vases communiquants à l'équilibre soient tous remplies jusqu'à la même hauteur.
Profil de pression dans l'eau
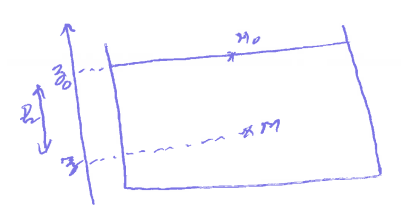
Entre \(M_0\) et \(M\)
$$P_0+\rho g z_0=P(z)+\rho g z$$
$$\implies P(z)= P_0+\rho g(z_0-z)$$
$$P=P_0+\rho g h$$
\(P\) croît linéairement avec la profondeur \(h\).
Cas d'un fluide compressible
On se place dans le cas d'un référentiel galiléen à une pesanteur uniforme, dans l'air en équilibre et isotherme (Comportement du gaz parfait).
On cherche la pression en tout point \(z\).
$$\vec{grad}=\rho\vec g$$ (
Equation de la statique des fluides)
$$dP=-\rho.g.dz$$
Avec \(\rho\) qui dépend de la pression car nous somme dans un fluide compressible.
Equation du gaz parfait (
Equation des gaz parfaits):
$$P.V=n.R.T$$
Avec: \(n=\frac mM\)
On a:
$$\rho=\frac{PM}{RT}$$
Par conséquent:
$$dP=-\frac{PMg}{RT}dz$$
On veut maintenant intégrer:
$$\frac {dP}P=-\frac{Mg}{RT}dz$$
$$d(ln(P))=-\frac{Mg}{RT}dz$$
$$\implies [ln(P)]_{p_0}^{P(z)}=-\frac{Mg}{RT}[z]_0^z$$
$$ln(\frac{P(z)}{P_0})=-\frac{Mg}{RT}z$$
$$P(z)=P_0e^{\frac{Mg}{RT}z }$$
On peut poser \(z_0=\frac{RT}{Mg}\) en \(mètre\):
$$\bbox[5px, border: 2px solid red]{P(z)=P_0e^\frac z{z_0} }$$
Poussée d'Archimède
Poussée d'Archimède

